2021-05-24

modについて（逆元の計算）

$5d \equiv 1 \ (\rm mod\ 96)$ において、 $1 < d < 96$ を満たす $d$ を求める。
5は96を法として逆元 $d$ を持つという言い方をする。

$5 = 1 \cdot 96 -91$
であるので、
$5 \equiv -91 \ (\rm mod\ 96)$
従って、
$-91d \equiv 1\ (\rm mod\ 96)$
と表せる。
よって、連立方程式を解けば、
${\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} 5d \equiv 1 \ (\rm mod\ 96) \\ -91d \equiv 1\ (\rm mod\ 96) \end{array} \right. \end{eqnarray} }$

$d = -19$
となる。これも逆元の一つだが、
$1 < d < 96$ を満たすことが条件なので、
$d = -19+96=77$
と求められる。

$5\cdot-19 \equiv 5\cdot77 \equiv 1 \ (\rm mod\ 96)$

2021-04-14

django 設定手順

djangoは最初の設定手順が多く覚えられないのでメモ
前回作った仮想通貨のチャートを表示するwebアプリを作る

プロジェクトの作成

django-admin startproject chart_prj

作成したプロジェクトフォルダにtemplatesとstaticという名のフォルダを作成

cd chart_prj
mkdir templates
mkdir static

chart_prjの中のsettings.pyにtemplatesフォルダを紐づける

TEMPLATES = [
    {
        'BACKEND': 'django.template.backends.django.DjangoTemplates',
        'DIRS': [os.path.join(BASE_DIR, 'templates')],    <--------ここ！
        'APP_DIRS': True,
        'OPTIONS': {
            'context_processors': [
                'django.template.context_processors.debug',
                'django.template.context_processors.request',
                'django.contrib.auth.context_processors.auth',
                'django.contrib.messages.context_processors.messages',
            ],
        },
    },
]

そのままsettings.pyの一番下にstaticフォルダを紐づける記述を追加

STATICFILES_DIRS = (
    os.path.join(BASE_DIR, 'static'),
)

表示するhtmlを作成し、templatesの中へ入れる
index.htmlの中身

<html>
<head>
<title>staticfile test</title>
<style>
p.chart_png img{width: 100%}
</style>
</head>
<body>
    <p class="chart_png">
          {% load static %}
          <img src="{% static "chart.png" %}">
    </p>
</body>
</html>

index.htmlで表示するchart.pngをstaticの中へ入れる

一通りフォルダを作ったりファイルを置いたりが終了

webアプリを作成

python manage.py startapp drawapp

settings.pyのINSTALLED_APPSにアプリを追加

INSTALLED_APPS = [
    'django.contrib.admin',
    'django.contrib.auth',
    'django.contrib.contenttypes',
    'django.contrib.sessions',
    'django.contrib.messages',
    'django.contrib.staticfiles',
    'drawapp',     <-------ここ！
]

INSTALEED_APPSに何かものを追加したらmigrateする

python manage.py migrate

drawappの中のviews.pyにindex.htmlを呼ぶプログラムを書く

from django.shortcuts import render
 
def index_template(request):
    return render(request, 'index.html')

drawappの中にurls.pyを作り、中身を次のように書く

from django.urls import path
from . import views

urlpatterns = [
    path('templates/', views.index_template, name='index_template'),
]

chart_prjの中にもurls.pyがあるので、上記のurls.pyを参照できるように追加で記述

from django.contrib import admin
from django.urls import path, include     <---------ここ！
 
urlpatterns = [
    path('admin/', admin.site.urls),
    path('drawapp/', include('drawapp.urls')),     <---------ここ！
]

ここまででローカルでのwebアプリ作成が終了
サーバーを立ち上げて確認

python manage.py runserver

http://localhost:8000/drawapp/templates
にアクセスし、正しくchart.pngが表示されることを確認

herokuにデプロイするための準備

Procfileというファイルを作りchart_prjのルートに配置
Procfileの中身

web: gunicorn chart_prj.wsgi --log-file -

runtime.txtを作りchart_prjのルートに配置
runtime.txtの中身

python-3.7.10

chart_prjのルートに仮想環境を設置

python -m venv chart_env

仮想環境をアクティベート

source chart_env/bin/activate

必要なライブラリを仮想環境にインストール

pip install django whitenoise gunicorn

herokuにログインする

heroku login

ブラウザが起動するので、ログインボタンをクリックする

heroku上にwebアプリを格納する場所を作る

heroku create chart-page

作った場所のWeb URLを確認する

heroku apps:info chart-page

settings.pyを編集

# SECURITY WARNING: don't run with debug turned on in production!
DEBUG = False       <---------ここ！

ALLOWED_HOSTS = ['chart-page.herokuapp.com', '127.0.0.1']        <-----------ここ！


# Application definition

INSTALLED_APPS = [
    'django.contrib.admin',
    'django.contrib.auth',
    'django.contrib.contenttypes',
    'django.contrib.sessions',
    'django.contrib.messages',
    'django.contrib.staticfiles',
    'drawapp',
]

MIDDLEWARE = [
    'django.middleware.security.SecurityMiddleware',
    'django.contrib.sessions.middleware.SessionMiddleware',
    'django.middleware.common.CommonMiddleware',
    'django.middleware.csrf.CsrfViewMiddleware',
    'django.contrib.auth.middleware.AuthenticationMiddleware',
    'django.contrib.messages.middleware.MessageMiddleware',
    'django.middleware.clickjacking.XFrameOptionsMiddleware',
    'whitenoise.middleware.WhiteNoiseMiddleware',                <--------------ここ！
]

settings.pyの一番下のSTATICの設定も変更
STATICFILES_DIRSはコメントアウトし、STATIC_ROOTを追加

# Static files (CSS, JavaScript, Images)
# https://docs.djangoproject.com/en/3.1/howto/static-files/

STATIC_URL = '/static/'
"""
STATICFILES_DIRS = (
    os.path.join(BASE_DIR, 'static'),
)
"""
STATIC_ROOT = os.path.join(BASE_DIR, 'static')           <------------ここ！

下のコマンドで静的ファイルを一箇所にまとめる

python manage.py collectstatic

staticフォルダにadminフォルダが生成されているのを確認

ブラウザ上のherokuから作成したアプリを開き、settingsをクリック
右下Add BuildpackをクリックしてPythonを選びsave changesをクリック
メニューバーのDeployをクリック

chart_prjのルートにリポジトリを作成し、herokuにセット

git init
heroku git:remote -a chart-page

herokuのリモートリポジトリに、変更点をaddして、commitし、push
git add . の「.」は全てのファイルをまとめて追加という意味

git add .
git commit -am "first commit"
git push heroku master

pushに失敗したら下のコマンドを実行し、再度push

heroku config:set DISABLE_COLLECTSTATIC=1

https://chart-page.herokuapp.com/drawapp/templates/
にアクセスし、chart.pngが表示されることを確認

以上

2021-04-10

仮想通貨の自動取引　チャート作成

仮想通貨で勝手に金を稼ぎ出すロボットを作ります。まずは、チャートを作るプログラムを作りました。
BinanceのAPIを使って、価格情報を得ています。

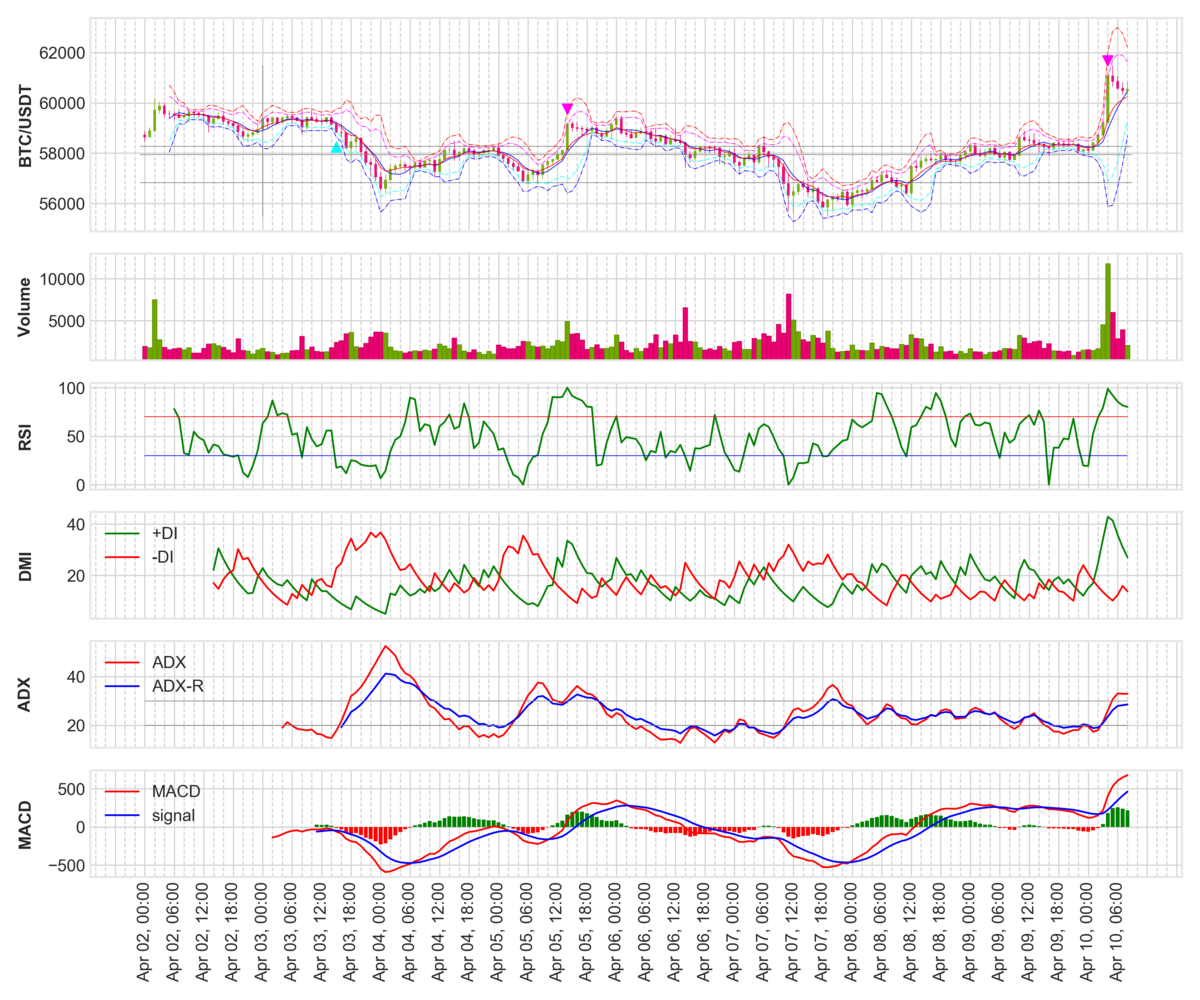
f:id:ryuuseigo:20210410180226p:plain — BTC/USDT

from binance.client import Client
import time
import numpy as np
import pandas as pd
import datetime
from pytz import timezone
import mplfinance as mpf
from matplotlib.ticker import MultipleLocator

class ChartGen(object):
    def __init__(self, start_date):
        API_KEY = '****************************************'
        API_SECRET = '****************************************'
        self.client = Client(API_KEY, API_SECRET)
        self.start_date = start_date # start_dateから現在までのOHLCを取得
    
    def get_df(self):
        klines = self.client.get_historical_klines(symbol='BTCUSDT', interval='1h', start_str=self.start_date)
        # klinesの各要素のlistのカラム
        klines_columns = ['Open time',
                          'Open',
                          'High',
                          'Low',
                          'Close',
                          'Volume',
                          'Close time',
                          'Quote asset volume',
                          'Number of trades',
                          'Taker buy base asset volume',
                          'Taker buy quote asset volume',
                          'Can be ignored']
        klines_df = pd.DataFrame(index=[], columns=klines_columns)
        for i in range(len(klines)):
            # 取得したklineはint型とstring型が混在しているので、全部float型にする
            klines_f = [float(klines[i][j]) for j in range(len(klines[i]))]
            # binance APIのtimestampは13桁であるのに対し、pythonのUNIX時間は10桁であるので、biannceのUNIX時間を1000で割る
            klines_f[0] = datetime.datetime.fromtimestamp(klines_f[0]/1000, datetime.timezone.utc)
            # listをSeriesに変換してから、DateFrameにappendする
            kline_s = pd.Series(klines_f, index=klines_df.columns)
            klines_df = klines_df.append(kline_s, ignore_index=True)
        klines_df.set_index('Open time', inplace=True)
    
        df = klines_df.loc[:,['Open', 'High', 'Low', 'Close', 'Volume']]
        return df


    def get_ma(self, data, n):
        # 単純移動平均の計算
        # nは移動平均の期間(4時間足でn=6なら期間は1日となる)
        
        ma = np.zeros(len(data))
        for i in range(len(data)):
            if i < n-1:
                ma[i] = np.nan # n個のデータが集まるまでは、np.nan
            else:
                ma[i] =  np.mean(data[i-(n-1):i+1])
        return ma
    
    
    def get_ema(self, data, n):
        # 指数移動平均の計算
        # nは移動平均の期間(4時間足でn=6なら期間は1日となる)
        # 先頭から連続するnan以外の欠損値がある場合、計算不可となるから注意
        
        nan_count = np.count_nonzero(np.isnan(data)) # 先頭からのnanの数を予め数えておく
        ema = np.zeros(len(data))
        alpha = 2 / (n + 1)
        for i in range(len(data)):
            if i < nan_count+n-1:
                ema[i] = np.nan # n個のデータが集まるまでは、np.nan
            elif i == nan_count+n:
                ema[i] = np.mean(data[i-(n-1):i+1])
            else:
                ema[i] = ema[i-1] + alpha * (data[i] - ema[i-1])
        return ema
    
    
    def get_bb(self, df, n):
        # ボリジャーバンドの計算
        # 単純移動平均から標準偏差を計算する
        
        ma = np.zeros(len(df))
        bb_std = np.zeros(len(df))
        for i in range(len(df)):
            if i < n-1:
                ma[i] = np.nan
                bb_std[i] = np.nan
            else:
                ma[i] =  np.mean(df['Close'][i-(n-1):i+1])
                bb_std[i] = np.std(df['Close'][i-(n-1):i+1])
                
        bb_dict = {'BB_2sigma_upper': ma + 2*bb_std,
                   'BB_2sigma_lower': ma - 2*bb_std,
                   'BB_3sigma_upper': ma + 3*bb_std,
                   'BB_3sigma_lower': ma - 3*bb_std}
        return bb_dict
    
    
    def get_rsi(self, df, n):
        # RSI(Relative Strength Index)の計算
        
        # diffは終値の差分
        diff = np.zeros((len(df)-1, 2)) # 差分なので0番目の要素は計算されないので要素数-1、さらに上昇と下降で分ける
        for i in range(len(df)-1):
            diff_ = df['Close'][i+1] - df['Close'][i]
            if diff_ > 0:
                diff[i,0] = diff_
            else:
                diff[i,1] = diff_

        diff_ma = [self.get_ma(diff[:,0], n), np.abs(self.get_ma(diff[:,1], n))]
        
        RSI = 100 * diff_ma[0] / (diff_ma[0] + diff_ma[1])
        RSI = np.insert(RSI, 0, np.nan) #要素数が足りないので、先頭にNanを追加
        return RSI


    def get_dmi(self, df):
        # DMI(Directional Movement Index)の計算
        # 現在の相場がボックスかトレンドかの判断に有効な指標
        # +DIは上昇の強さ, -DIは下降の強さ、ADXはトレンドの強さを表す
        # ADXがADX-Rを下から上抜いた時 -> トレンドが強い
        # ADXがADX-Rを上から下抜いた時 -> トレンドが弱い
        
        # +DM, -DMの計算
        pDM = np.zeros(len(df))
        nDM = np.zeros(len(df))
        for i in range(len(df)):
            if i == 0:
                pDM[i] = np.nan # 前日との差分からDMを計算するので先頭はnan
                nDM[i] = np.nan
            else:
                # +DM = 当日の高値 - 前日の高値 ただし、+DM<0の場合は0
                # -DM = 前日の安値 - 当日の安値 ただし、-DM<0の場合は0
                pDM[i] = np.max([df['High'][i] - df['High'][i-1], 0])
                nDM[i] = np.max([df['Low'][i-1] - df['Low'][i], 0])
    
                # 含み足の場合は+DMと-DMそれぞれで0以上の値となる為、値の大きい方を残して他方を0にする
                if nDM[i] >= pDM[i]:
                    pDM[i] = 0
                elif pDM[i] >= nDM[i]:
                    nDM[i] = 0

        # TRの計算
        TR = np.zeros(len(df))
        for i in range(len(df)):
            if i == 0:
                TR[i] = np.nan # 計算に前日のデータを使用するので先頭はnan
            else:
                # (当日の高値 - 当日の安値), (当日の高値 - 前日の終値), (前日の終値 - 当日の安値)
                # 上記の値で最大となるものをTRとする
                TR[i] = np.max([np.abs(df['High'][i]-df['Low'][i]),
                                np.abs(df['High'][i]-df['Close'][i-1]),
                                np.abs(df['Close'][i-1]-df['Low'][i])])

        # +DI, -DIの計算
        # 指数移動平均を使う（関数を使おうとすると逆に複雑なので、そのまま計算）
        pDI = np.zeros(len(df))
        nDI = np.zeros(len(df))
        n = 14 # 移動平均の期間(ワイルダーは期間14を推奨している)
        alpha = 2 / (n +1)
        for i in range(len(df)):
            if i < n-1:
                pDI[i] = np.nan
                nDI[i] = np.nan
            elif i == n:
                pDI[i] = (np.mean(pDM[i-(n-1):i+1]) / np.mean(TR[i-(n-1):i+1])) * 100
                nDI[i] = (np.mean(nDM[i-(n-1):i+1]) / np.mean(TR[i-(n-1):i+1])) * 100
            else:
                pDI[i] =  pDI[i-1] + alpha * (((pDM[i] / TR[i])*100) - pDI[i-1])
                nDI[i] =  nDI[i-1] + alpha * (((nDM[i] / TR[i])*100) - nDI[i-1])

        # ADXの計算
        DX = np.abs(pDI - nDI) / (pDI + nDI) * 100
        
        # DXの指数移動平均でADXを計算
        n_adx = 14 # ADXにおける移動平均の期間はDIとは異なる期間を用いることができる(ワイルダーはDIの計算に使った期間と同じ期間を推奨している)
        ADX = self.get_ema(DX, n_adx)
        # ADX-Rの計算
        n_adx_r = 26 #ADX-Rの移動平均に用いる期間はADXよりも長くする
        ADX_R = self.get_ema(DX, n_adx_r)
        
        DMI_dict = {'+DI': pDI,
                    '-DI': nDI,
                    'ADX': ADX,
                    'ADX-R': ADX_R}
        return DMI_dict


    def get_macd(self, df):
        # MACDの計算
        # MACDは価格の変化に敏感
        # MACDシグナルは価格の変化に鈍感
        # MACDがMACDシグナルを下から上抜いた時 -> 買い
        # MACDがMACDシグナルを上から下抜いた時 -> 売り
        
        # MACDは期間12と期間26の指数移動平均の差分
        ema_12 = self.get_ema(df['Close'], 12)
        ema_26 = self.get_ema(df['Close'], 26)
        MACD = ema_12 - ema_26

        # シグナルの計算
        # シグナルはMACDの期間9の指数移動平均で計算する
        signal = self.get_ema(MACD, 9)
        
        # MACDとシグナルの差を計算
        bar = np.zeros((len(MACD), 2))
        for i in range(len(MACD)):
            diff = MACD[i] - signal[i]
            if diff >= 0:
                bar[i,0] = diff
                bar[i,1] = np.nan
            elif diff < 0:
                bar[i,1] = diff
                bar[i,0] = np.nan
            else:
                bar[i,:] = np.nan
        
        MACD_dict = {'MACD': MACD,
                     'signal': signal,
                     'bar_high': bar[:,0],
                     'bar_low': bar[:,1]}
        return MACD_dict
    
    
    def get_signal(self, df):
        # RSI>70% かつ 2sigma を超えたときは買われすぎ
        # RSI<30% かつ -2sigma を超えたときは売られすぎ
        # ボックス相場で有効な指標
        # ADX < 40% でボックス相場と判断する
        signal = np.zeros((len(df), 2))
        for i in range(len(df)):
            if df['Close'][i] > df['BB_2sigma_upper'][i] and df['RSI'][i] > 70 and df['ADX'][i] < 40:
                signal[i,0] = df['Close'][i] * 1.01
                signal[i,1] = np.nan
            elif df['Close'][i] < df['BB_2sigma_lower'][i] and df['RSI'][i] < 30 and df['ADX'][i] < 40:
                signal[i,1] = df['Close'][i] * 0.99
                signal[i,0] = np.nan
            else:
                signal[i,:] = np.nan

        signal_dict = {'high': signal[:,0],
                       'low': signal[:,1]}
        return signal_dict


    def add_indicator(self, df):
        # データフレームに指標を追加
        df['MA'] = self.get_ma(df['Close'], 6)
        df['EMA'] = self.get_ema(df['Close'], 6)
        
        bb = self.get_bb(df, 6)
        df['BB_2sigma_upper'] = bb['BB_2sigma_upper']
        df['BB_2sigma_lower'] = bb['BB_2sigma_lower']
        df['BB_3sigma_upper'] = bb['BB_3sigma_upper']
        df['BB_3sigma_lower'] = bb['BB_3sigma_lower']
        
        df['RSI'] = self.get_rsi(df, 6)
        df['RSI_70'] = np.full(len(df), 70)
        df['RSI_30'] = np.full(len(df), 30)
        
        DMI = self.get_dmi(df)
        df['+DI'] = DMI['+DI']
        df['-DI'] = DMI['-DI']
        df['ADX'] = DMI['ADX']
        df['ADX-R'] = DMI['ADX-R']
        df['ADX_20'] = np.full(len(df), 20) # 20%<ADX<30%のラインを書く
        df['ADX_30'] = np.full(len(df), 30)
        
        MACD = self.get_macd(df)
        df['MACD'] = MACD['MACD']
        df['MACD_signal'] = MACD['signal']
        df['MACD_bar_high'] = MACD['bar_high']
        df['MACD_bar_low'] = MACD['bar_low']
        
        signal = self.get_signal(df)
        df['signal_high'] = signal['high']
        df['signal_low'] = signal['low']
        return df


    def draw_fig(self):
        df = self.get_df()
        df = self.add_indicator(df)

        fig = mpf.figure(figsize=(12,10),style='binance', tight_layout=True)

        heights = [2,1,1,1,1,1] # fig.add_gridspecで指定する各axの高さの比率
        gs = fig.add_gridspec(6,1, height_ratios=heights) # 3行1列のgridspecを作成

        ax1 = fig.add_subplot(gs[0,0]) # 1行1列にプロット
        ax2 = fig.add_subplot(gs[1,0], sharex=ax1) # 2行1列目にプロットし、sharex=ax1でax1とx軸を共通化
        ax3 = fig.add_subplot(gs[2,0], sharex=ax1)
        ax4 = fig.add_subplot(gs[3,0], sharex=ax1)
        ax5 = fig.add_subplot(gs[4,0], sharex=ax1)
        ax6 = fig.add_subplot(gs[5,0], sharex=ax1)

        adps = [mpf.make_addplot(df['MA'], ax=ax1, color='blue', width=0.5),
                mpf.make_addplot(df['EMA'], ax=ax1, color='red', width=0.5),
                mpf.make_addplot(df['BB_2sigma_upper'], ax=ax1, linestyle='dashdot', color='magenta', width=0.5),
                mpf.make_addplot(df['BB_2sigma_lower'], ax=ax1, linestyle='dashdot', color='cyan', width=0.5),
                mpf.make_addplot(df['BB_3sigma_upper'], ax=ax1, linestyle='dashdot', color='red', width=0.5),
                mpf.make_addplot(df['BB_3sigma_lower'], ax=ax1, linestyle='dashdot', color='blue', width=0.5),
                mpf.make_addplot(df['signal_high'], ax=ax1, type='scatter', markersize=50,marker='v', color='magenta'),
                mpf.make_addplot(df['signal_low'], ax=ax1, type='scatter', markersize=50,marker='^', color='cyan'),                 
                mpf.make_addplot(df['RSI'], ax=ax3, color='green', ylabel='RSI'),
                mpf.make_addplot(df['RSI_70'], ax=ax3, color='red', width=0.5),
                mpf.make_addplot(df['RSI_30'], ax=ax3, color='blue', width=0.5),
                mpf.make_addplot(df['+DI'], ax=ax4, color='green', ylabel='DMI'),
                mpf.make_addplot(df['-DI'], ax=ax4, color='red'),
                mpf.make_addplot(df['ADX'], ax=ax5, color='red', ylabel='ADX'),
                mpf.make_addplot(df['ADX-R'], ax=ax5, color='blue', ylabel='ADX'),
                mpf.make_addplot(df['ADX_20'], ax=ax5, color='gray', width=0.5),
                mpf.make_addplot(df['ADX_30'], ax=ax5, color='gray', width=0.5),
                mpf.make_addplot(df['MACD'], ax=ax6, color='red', ylabel='MACD'),
                mpf.make_addplot(df['MACD_signal'], ax=ax6, color='blue'),
                mpf.make_addplot(df['MACD_bar_high'], type='bar', ax=ax6, color='green'),
                mpf.make_addplot(df['MACD_bar_low'], type='bar', ax=ax6, color='red')]

        vlines = ['2021-04-03 00:00:00']
        hlines = [57941, 58270, 56830]

        mpf.plot(df,ax=ax1,
                 type='candle',
                 ylabel='BTC/USDT',
                 volume=ax2,
                 addplot=adps,
                 vlines=dict(vlines=vlines, colors='gray', linewidths=[0.1]),
                 hlines=dict(hlines=hlines, colors='gray', linewidths=[0.1]),
                 returnfig=True)

        ax1.tick_params(labelbottom=False) # x軸のラベルを表示しない
        ax2.tick_params(labelbottom=False)
        ax3.tick_params(labelbottom=False)
        ax4.tick_params(labelbottom=False)
        ax5.tick_params(labelbottom=False)
        ax6.tick_params(axis='x', labelrotation=90) # x軸のラベルを90度回転
        ax4_legend=['+DI', '-DI']
        ax5_legend=['ADX', 'ADX-R']
        ax6_legend=['MACD', 'signal']
        ax4.legend(ax4_legend, loc='upper left')
        ax5.legend(ax5_legend, loc='upper left')
        ax6.legend(ax6_legend, loc='upper left')

        fig.align_labels([ax1, ax2, ax3, ax4, ax5, ax6])
        
        ax1.xaxis.set_major_locator(MultipleLocator(6))
        ax1.xaxis.set_minor_locator(MultipleLocator(2))
        ax1.grid(True, which='major', linestyle='-')
        ax1.grid(True, which='minor', linestyle='--')
        ax2.grid(True, which='major', linestyle='-')
        ax2.grid(True, which='minor', linestyle='--')
        ax3.grid(True, which='major', linestyle='-')
        ax3.grid(True, which='minor', linestyle='--')
        ax4.grid(True, which='major', linestyle='-')
        ax4.grid(True, which='minor', linestyle='--')
        ax5.grid(True, which='major', linestyle='-')
        ax5.grid(True, which='minor', linestyle='--')
        ax6.grid(True, which='major', linestyle='-')
        ax6.grid(True, which='minor', linestyle='--')        

        mpf.show()
        fig.savefig('chart.png', dpi=300)

if __name__ == "__main__":
    
    start_date = '2021-04-02 00:00:00'
    chart = ChartGen(start_date)
    chart.draw_fig()

2021-02-22

ESP-01とDHT11を使ったサーバー

ESP-01の使い方が分かったので、温度センサーDHT11を組み合わせて、部屋の温度をサーバーから確認できるようにします。

回路図

f:id:ryuuseigo:20210222153442p:plain — 回路図

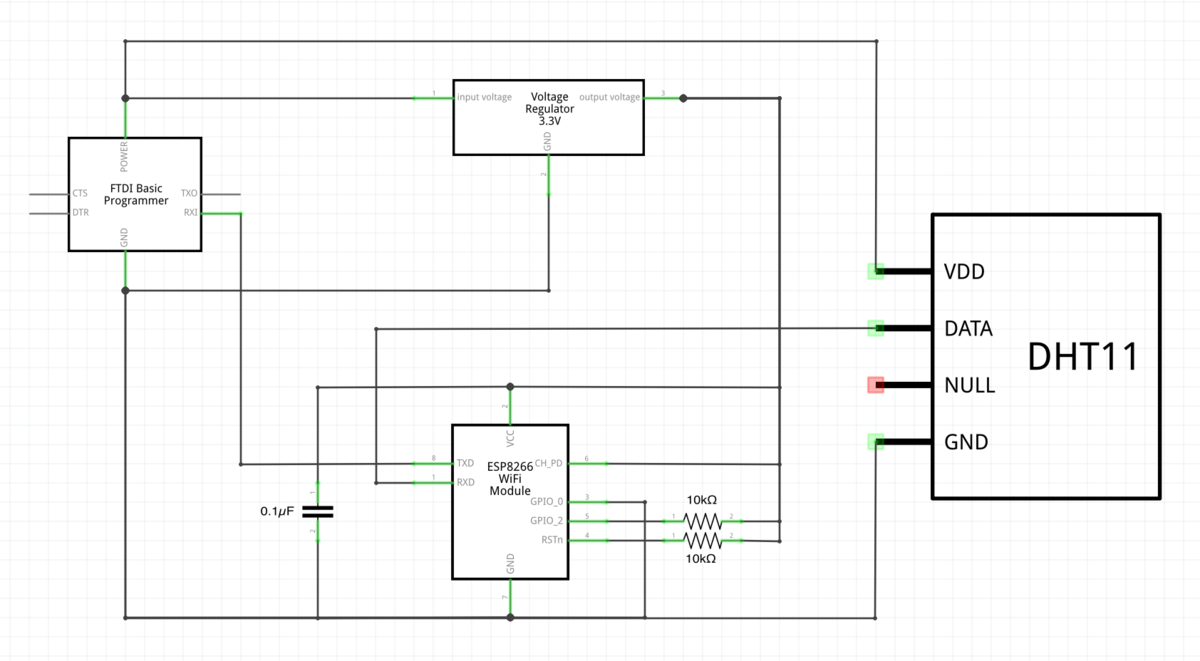
DHT11は3.3V〜5.5Vの間で使えるそうなので、5Vで使うことにしました。
DHT11のデータピンはESP-01のRXに接続することで、ウェブサーバー上からDHT11の値を確認できるようになります。
ESP-01のTXとFTDIのRXを接続することで、シリアルモニタからも値を確認できます。

プログラム

#include <stdio.h>
#include <ESP8266WiFi.h>
#include <WiFiClient.h>
#include <ESP8266WebServer.h>
#include <DHT.h>

#ifndef APSSID
#define APSSID "ESP01"
#define APPSK  "123456789"
#define DHTPIN 3 //DHTのDATAピンはESP-01のRXに接続
#define DHTTYPE DHT11
#endif

/* Set these to your desired credentials. */
const char *ssid = APSSID;
const char *password = APPSK;

DHT dht(DHTPIN, DHTTYPE);

ESP8266WebServer server(80);

/* Just a little test message.  Go to http://192.168.4.1 in a web browser
   connected to this access point to see it.
*/

float h; //湿度
float t; //気温（摂氏）
float f; //気温（華氏)

String form; //htmlを書き込む変数

/* プロトタイプ宣言 */
void handleRoot();
void dht_sensor();
void get_form();

void setup() {
  delay(1000);
  Serial.begin(115200);
  Serial.println();
  Serial.print("Configuring access point...");
  /* You can remove the password parameter if you want the AP to be open. */
  WiFi.softAP(ssid, password);

  IPAddress myIP = WiFi.softAPIP();
  Serial.print("AP IP address: ");
  Serial.println(myIP);
  server.on("/", handleRoot);
 
  server.begin();
  Serial.println("HTTP server started");

  dht.begin();
  Serial.println("DHT11 started");
  
}

void dht_sensor() {
  // Wait a few seconds between measurements.
  delay(2000);

  // Reading temperature or humidity takes about 250 milliseconds!
  // Sensor readings may also be up to 2 seconds 'old' (its a very slow sensor)
  h = dht.readHumidity();
  // Read temperature as Celsius (the default)
  t = dht.readTemperature();
  // Read temperature as Fahrenheit (isFahrenheit = true)
  f = dht.readTemperature(true);

  // Check if any reads failed and exit early (to try again).
  if (isnan(h) || isnan(t) || isnan(f)) {
    Serial.println(F("Failed to read from DHT sensor!"));
    return;
  }

  // Compute heat index in Fahrenheit (the default)
  float hif = dht.computeHeatIndex(f, h);
  // Compute heat index in Celsius (isFahreheit = false)
  float hic = dht.computeHeatIndex(t, h, false);

  Serial.print(F("Humidity: "));
  Serial.print(h);
  Serial.print(F("%  Temperature: "));
  Serial.print(t);
  Serial.print(F("°C "));
  Serial.print(f);
  Serial.print(F("°F  Heat index: "));
  Serial.print(hic);
  Serial.print(F("°C "));
  Serial.print(hif);
  Serial.println(F("°F"));
}

/*formにhtml文を書き込む*/
void get_form() {
  form = 
  "<!doctype html>"
  "<html><head><meta charset=\"UTF-8\"/>"
  "<meta name=\"viewport\" content=\"width=device-width\"/>"
  "</head><body>"
  "湿度:"
  + String(h) +"%"
  "<br>"
  "気温:"
  + String(t) + "°C"
  "</body></html>";
}

void handleRoot() {
  dht_sensor();
  get_form();
  server.send(200, "text/html", form);
}

void loop() {
  dht_sensor();
  server.handleClient();
}

iPhoneからサーバーにアクセスすると非常にシンプルな画面が表示されます。

f:id:ryuuseigo:20210222154530j:plain — iPhoneの画面

このプログラムはブラウザの更新ボタンを押さないと値が更新されません。次は自動更新のプログラムを追加したいと思います。

2021-02-20

ESP-01の使い方

ESP-01はプログラムを書き込めるWi-Fiモジュールです。これを使って魚群探知機を作ることを目標にしたいと思います。

f:id:ryuuseigo:20210220162100p:plain — ESP-01の外観

使い方

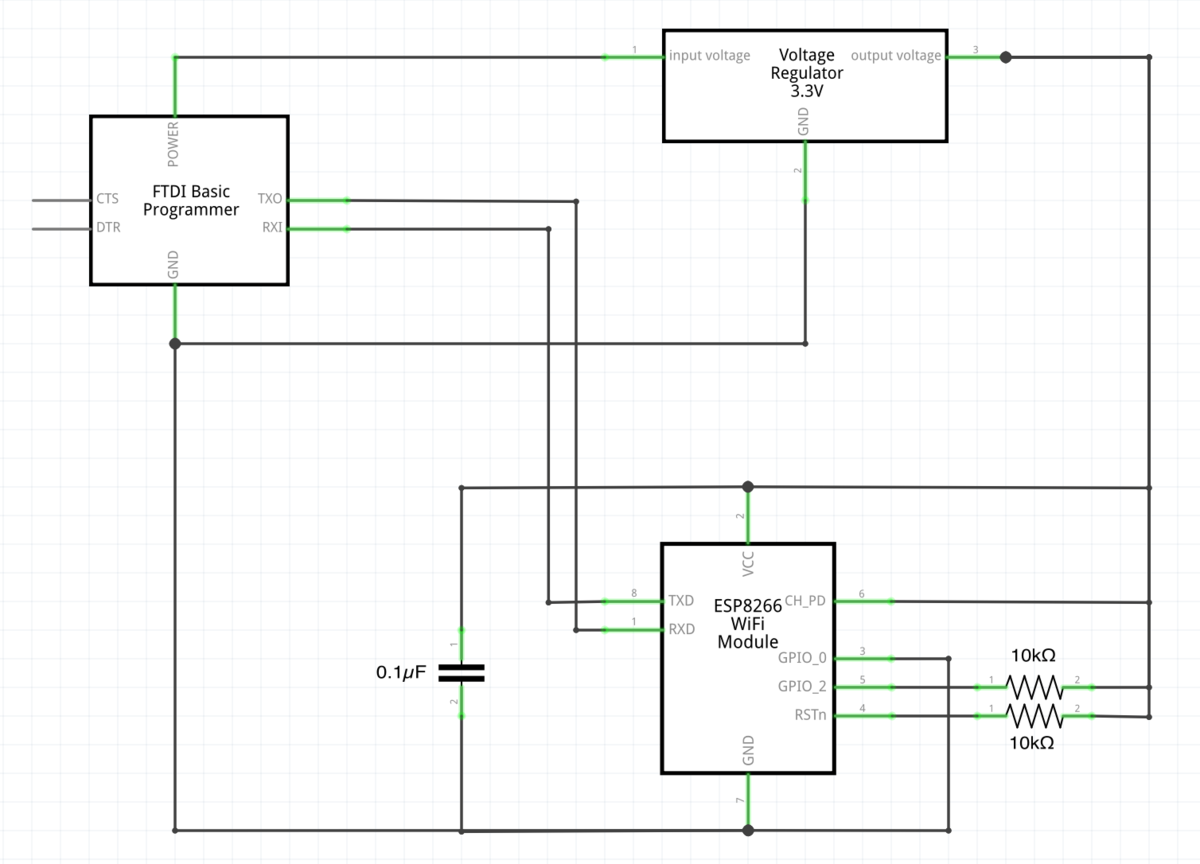
f:id:ryuuseigo:20210220215929p:plain — プログラム時の回路図

プログラム時
GPIO_0: Low
GPIO_2: High プルアップ抵抗10kΩを挟む
CH_PD: High
RSTn: High プルアップ抵抗10kΩを挟む
FTDIとESP-01のTX,RXはクロス結線であることに注意！
ESP-01は電源3.3Vをシビアに要求するそうなので、レギュレータで3.3Vにする＋コンデンサをVccとGNDに並列接続（デカップリングコンデンサというらしい）しました。

通常動作時
GPIO_0: High プルアップ抵抗10kΩを挟む
GPIO_2: High プルアップ抵抗10kΩを挟む
CH_PD: High
RSTn: High プルアップ抵抗10kΩを挟む
TXD → GPIO 1番
RXD → GPIO 3番

データシートを見たのでメモ
・GPIO_0とGPIO_2はプルアップして使う。
・CH_PDはチップ有効ピン。Highで有効。
・RSTnはリセットピン。Lowでリセット。
・GPIO_0をプログラム時にLowとするとUART（非同期式シリアル通信）が有効になる。

2020-12-13

強化学習の勉強　方策勾配法でMountainCarを試す

OpenAI Gym 入門 - Qiita
この方の記事を参考に方策勾配法でMountainCarを試しました。

強化学習の勉強をする上で環境（ゲーム）を作るが大変だったのですが、OpenAIのgymは一瞬で環境を構築できるので感動しました。

使うのはこれだけ

import gym
import numpy as np

環境はこれで定義します。
他にも色々な環境が用意されていたので、後日試したいと思います。

env = gym.make('MountainCar-v0')

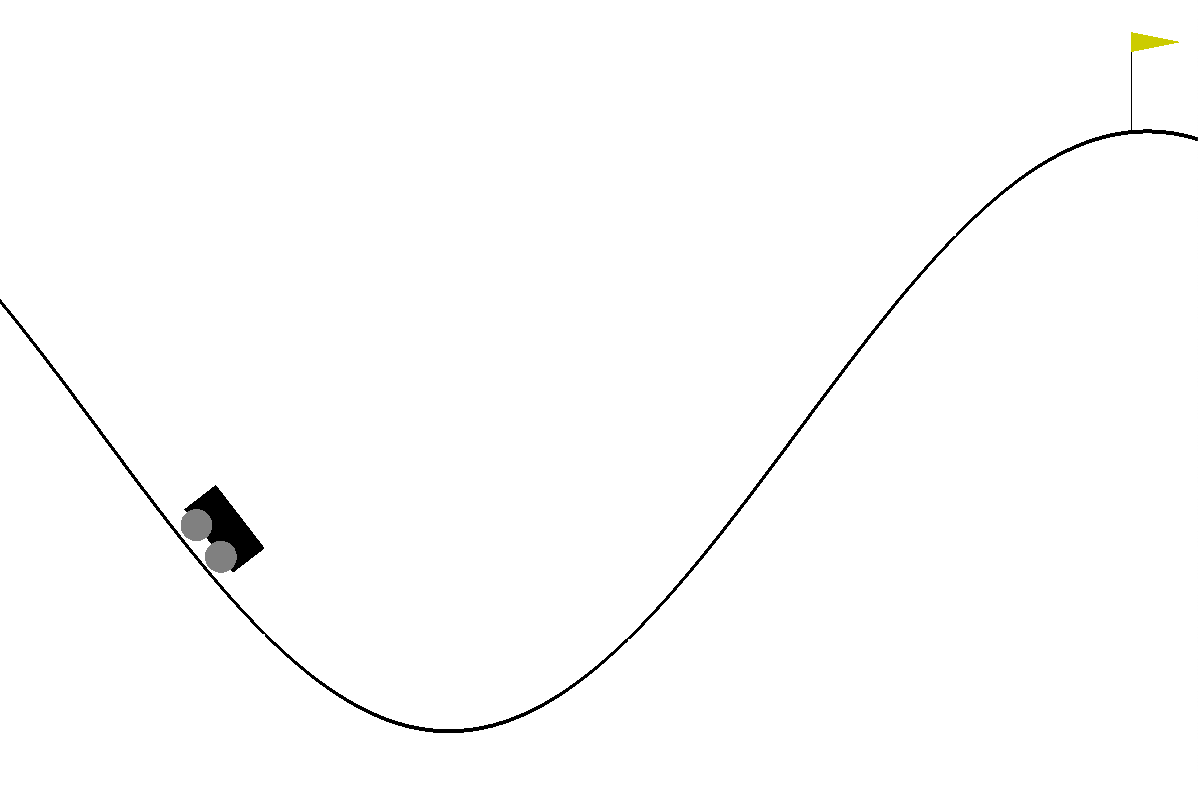
f:id:ryuuseigo:20201213132513p:plain — 環境

この環境は２つの山に囲まれた谷から車を脱出させるというゲームですが、車のエンジンが弱い為、重力を利用しながら加速してゴールを目指さなくてはなりません。

状態は
・位置: -1.2〜0.6 （位置が0.5よりも大きくなったらゴール）
・速度: -0.07〜0.07

行動は
・[0]で左にアクセル
・[1]でなにもしない
・[2]で右にアクセル

env.step(action)

で状態、報酬、ゲーム終了フラグ、詳細情報を取り出せます。

MountainCarの場合は報酬は常に-1で、200ステップ経つと強制終了です。
200ステップ以内にゴールすることを目指します。

環境の初期化は

env = gym.make('MountainCar-v0')

で行います。

得られる状態は連続値であるため、40個の離散値に変換します。上で紹介した記事と同じです。

def get_status(observation):
    env_low = env.observation_space.low # 位置と速度の最小値
    env_high = env.observation_space.high #　位置と速度の最大値
    env_dx = (env_high - env_low) / 40 # 40等分
    # 0〜39の離散値に変換する
    position = int((observation[0] - env_low[0])/env_dx[0])
    velocity = int((observation[1] - env_low[1])/env_dx[1])
    return position, velocity

まずは方策のパラメータ $\theta$ を初期化します。
位置40個、速度40個、行動3個なので、方策のパラメータは $40 \times 40 \times 3$ の形状です。

theta = np.random.rand(40, 40, 3)

$\theta$ から方策 $\pi$ を得ます。
Softmax関数を用いて、各状態における各行動の確率を計算しています。
Softmaxは $\theta$ の値によってはオーバーフローを起こす可能性があるので、 $\theta$ の最大値を使って値を小さくします。
また、phi=1は今はよく理解していませんが、基底関数を定義することで何かいいことがあるみたい？？

def get_pi(theta):
    phi = 1
    [l, m, n] = theta.shape
    pi = np.zeros((l, m, n))
    
    for i in range(l):
        for j in range(m):
            for k in range(n):
                c = np.max(theta[i,j]) #オーバーフローを回避する為の定数
                pi[i,j,k] = np.exp(phi*(theta[i,j,k]-c)) / np.sum(np.exp(phi*(theta[i,j]-c)))
    return pi

現在の状態から行動を得ます。方策勾配法は、確率的方策なので確率に従って行動を選びます。
np.random.choiceでは確率の合計が1でなくてはならないのですが、数値誤差で1にならない可能性も考え、np.sumを使って強制的に合計値を1にしています。

def get_action(pi, observation):
    position, velocity = get_status(observation)
    action = np.random.choice([0,1,2], p=pi[position, velocity]/np.sum(pi[position, velocity]))
    return action

報酬関数を定義します。
MountainCarでは報酬が常に-1ですが、この報酬だとうまくいかなかったので、報酬関数を作りました。
現在の状態と1時刻前の状態の位置と速度の絶対値が報酬です。
また、ただ早く大きく動くだけでなく、ゴールを目指して欲しいので、ゴールに達したら特別に報酬を与えています。
報酬関数の設計の仕方で車の動きがかなり変わりました。
報酬関数の設計を強化学習させる逆強化学習なるものがあるそうなので、いずれ試したいと思います。

def reward_func(observation, _observation):
    position, velocity = get_status(observation)
    _position, _velocity = get_status(_observation)
    if position >= 37: #位置0.5以上でエピソードが終了である為、ゴールしたら特別に報酬を与える（位置0.5は37番目の状態）
        reward = np.abs(velocity - _velocity) + np.abs(position - _position) + 100
    else:
        reward = np.abs(velocity - _velocity) + np.abs(position - _position)
    return reward

方策勾配法では、M回Tステップのエピソードを使って、方策のパラメータ $\theta$ を更新します。
この方法をモンテカルロ近似というらしいです。
$\theta$ の更新式は
$\theta^{new} = \theta + \eta \nabla J(\theta)$
です。
$\eta$ は学習率、 $, \nabla J(\theta)$ は確率的方策の良さを量る量の勾配です。 $J(\theta)$ は割引報酬和の期待値で定義されるみたいです。
興味があるのは勾配なので、 $\nabla J(\theta)$ を計算します。
$\displaystyle \nabla J(\theta) \approx \frac{1}{M}\sum_{m=1}^{M}\frac{1}{T}\sum_{t=1}^{T}\nabla \log \pi(a_T^m|s_t^m)Q(s_t^m, a_t^m)$
$s_t^m$ と $a_t^m$ はmエピソード目のtステップ目の状態とそのときの行動です。
行動価値 $Q$ はなんらかの手法で近似しますが、今回は即時報酬で近似するREINFORCE アルゴリズムを使います。
ちなみに、行動価値 $Q$ はQ-learningで使うやつですが、環境がでかいとメモリを食いまくる為、そういう問題を扱うときは方策勾配法が選ばれるようです。
ロボットに強化学習させることを考えると、環境は位置X,Y,Z,W,R,Pだったり各軸値だったり、速度だったり、たしかにメモリを食いそうな環境だと思いました。

とにかく、なにも学習させずにM回のエピソードを回します。
R_listは各ステップの状態、行動、報酬を記録するリストです。
goal_countは後で学習結果を確認する為の記録用変数です。

def run_Mepisode(M, pi):
    R_list = []
    goal_count = 0
    
    for i in range(M):
        total_reward = 0
        observation = env.reset()
        
        R_log = []
        
        for j in range(200):
            # 現在の状態を取得
            position, velocity = get_status(observation)
            _observation = observation.copy()
            #env.render()
            # 行動を選択
            action = get_action(pi, _observation)

            # 車を動かし、観測結果・報酬・ゲーム終了FLG・詳細情報を取得
            observation, reward, done, _ = env.step(action)
            position, velocity = get_status(observation)
            reward = reward_func(observation, _observation)
            # nabla_J計算用に各ステップにおける状態、行動、報酬を記録
            R = np.array([position, velocity, action, reward])
            R_log.append(R)
            # 報酬の合計値を計算
            total_reward += reward
        
            if done:
                R_list.append(R_log)
                if j < 199:
                    goal_count += 1
                # doneがTrueになったら１エピソード終了
                break
    env.close()
    return R_list, total_reward, goal_count

M回のエピソードから色々データを取ってきたので、 $\nabla J(\theta)$ を計算します。
REINFORCE では、
$\displaystyle \nabla J(\theta) = \sum_{m=1}^{M}\sum_{t=1}^{T}(R_t^m - b)\nabla \log \pi(a_T^m|s_t^m)$
と計算します。
bは平均報酬で、
$\displaystyle b = \frac{1}{MT}\sum_{m=1}^{M}\sum_{t=1}^{T}R_t^m$
です。
R_listというリストが少々複雑なのですが、M回のエピソードについて各ステップでの状態（位置、速度）、行動、報酬が記録されています。
例えば、R_list[5]は6回目のエピソードにおける各ステップでの推移です。
R_list[5][3]とすれば、6回目のエピソードの4回目のステップでの状態、行動、報酬を見ることができます。
nabla_J[R_list[i][j][0], R_list[i][j][1], R_list[i][j][2]]は
R_list[i][j][0]が位置、
R_list[i][j][1]が速度、
R_list[i][j][2]が行動
である為、その状態におけるその行動の良さの勾配が要素となっています。

def get_nabla_J(pi, R_list):
    b = np.zeros((40,40,3))
    for i in range(len(R_list)):
        _b = np.zeros((40,40,3))
        for j in range(len(R_list[i])):
            _b[R_list[i][j][0], R_list[i][j][1], R_list[i][j][2]] += R_list[i][j][3]
        b += -b/len(R_list[i])
    b /= len(R_list)
    
    nabla_J = np.zeros((40,40,3))
    nabla_log_pi = 1-pi
    for i in range(len(R_list)):
        for j in range(len(R_list[i])):
            nabla_J[R_list[i][j][0], R_list[i][j][1], R_list[i][j][2]] += (R_list[i][j][3]- b[R_list[i][j][0], R_list[i][j][1], R_list[i][j][2]]) * nabla_log_pi[R_list[i][j][0], R_list[i][j][1], R_list[i][j][2]]
    return nabla_J

こうのような、プログラムにしたのですが悩んでいることがあります。
Softmaxの微分についてです。

$\mathbf{\theta} = [ \theta_1, \dots, \theta_n]^{\rm T}$
$\displaystyle S = Softmax = \frac{\exp(\theta_i)}{\sum \exp(\mathbf{\theta})}$
$\log S = \log \exp(\theta_i) - \log \sum \exp(\mathbf{\theta}) = \theta_i - \log \sum \exp(\mathbf{\theta})$

$\theta_i$ で微分
$i=j$ のとき
$\displaystyle \frac{\partial \log S}{\partial \theta_i} = 1 - \frac{1}{\sum \exp(\mathbf{\theta})}\exp(\theta_j) = 1 - S_i$
$i \neq j$ のとき
$\displaystyle \frac{\partial \log S}{\partial \theta_i} = - \frac{1}{\sum \exp(\mathbf{\theta})}\exp(\theta_i) = - S_i$

$\mathbf{\theta}=[\theta_i, \theta_j, \theta_k]$ のとき、 $\theta_i$ で微分すると $[1-S_i, -S_i, -S_i]$ となる。
従って、各 $\theta$ で微分すると、
$[1-S_i, -S_i, -S_i]$
$[-S_j, 1-S_j, -S_j]$
$[-S_k, -S_k, 1-S_k]$
となる。

$\theta$ の更新は
$\theta^{new} = \theta + \eta \nabla J(\theta)$
であるから、形を合わせる為に $i=j$ のときの $1-S$ だけを使うことにした。
つまり、
$\nabla J(\theta) = [ 1-S_i, 1-S_j, 1-S_k ]$
これが合ってるのか誰か教えて欲しい。。
うまく動いているぽかったので、たぶん合っているのだと信じます。

あとは、 $\theta$ を更新するだけです。

def update_theta(theta, nabla_J):
    eta = 0.1
    theta_ = theta.copy()
    theta = theta_ + eta * nabla_J
    return theta

gymではenv.render()というものを使うことで、ゲームの画面が表示されます。
結構楽しいので、学習後の車の動きを見られる関数も作っておきます。

def view_result(theta):
    pi = get_pi(theta)
    observation = env.reset()
    total_reward = 0
    step_count = 0
    
    while True:
        env.render()
        _observation = observation.copy()
        action = get_action(pi, _observation)
        observation, reward, done, _ = env.step(action)
        reward = reward_func(observation, _observation)
        total_reward += reward
        step_count += 1
        print("step: {} total_reward: {}".format(step_count, total_reward))
        if done:
            break
    env.close()

これで完成です。

if __name__ == '__main__':
    env = gym.make('MountainCar-v0')

    #方策のパラメータthetaを初期化
    theta = np.random.rand(40, 40, 3)
    result = []

    # M回のエピソードをN回繰り返す
    M = 20
    N = 500
    for i in range(N):
        observation = env.reset()
        pi = get_pi(theta)
        R_list, total_reward, goal_count = run_Mepisode(M, pi)
        nabla_J = get_nabla_J(pi, R_list)
        theta = update_theta(theta, nabla_J)
        result.append(goal_count)
        print("episode: {}/{} total_reward: {}".format(i*M, M*N, total_reward))

    # 5回動きを見る
    for i in range(5):
        view_result(theta)
    
    print(get_pi(theta))

# 結果の可視化
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(7,4), dpi=100)
ax.plot(result)
ax.grid()
plt.plot()

www.youtube.com

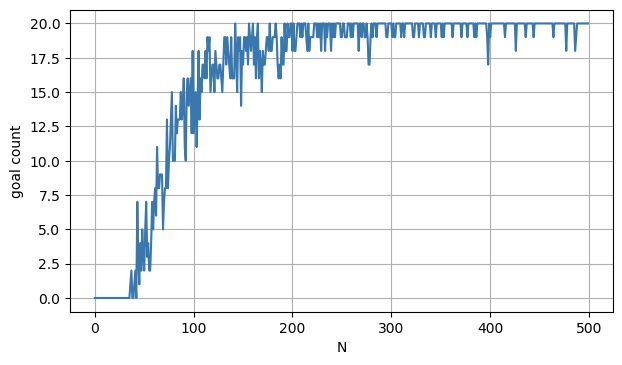
f:id:ryuuseigo:20201213202512p:plain — 学習結果

20回のエピソードを500回繰り返して学習した結果です。
おおよそ、4000(20エピソード×200回)あたりから、ほぼゴールにたどり着くようになりました。
ちなみに、報酬関数を使わず、-1で報酬を固定した場合は学習せず、行動1の何もしないを取り続けるだけでした。
報酬関数の次第で大きく結果が変わるということが分かりました。

2020-07-02

Swiftでガウス過程

ガウス過程回帰をSwiftで実装します。

ガウス過程は線形回帰の重みパラメータを積分消去し、カーネル関数（基底関数の内積）のみで関数を表現するモデルです。
確率モデルなので、予測に対する分散も表現できます。

Pythonで実装したものがあるので、これを参考にしてSwiftでも実行できるようにしたいと思います。

Calc()は前回の記事で作成した行列計算をまとめたクラスです。
今回は負の対数尤度、対数尤度をガウスカーネルの各ハイパーパラメータで微分したものまで書きました。

import Foundation

class GaussianProcess {
    let calc = Calc()
    let X: [[Double]]
    var theta: [Double]
    var y: [Double]
    
    
    init(X: [[Double]]){
        self.X = X
        self.theta = [Double.random(in: 0 ..< 1), Double.random(in: 0 ..< 1), Double.random(in: 0 ..< 1)]
        self.y = [Double](repeating: 0, count: X.count)
    }
    
    func kernel(X_i: [Double], X_j: [Double]) -> Double{
        let r: Double = calc.vsum(vector: calc.vpow(vector: calc.vmv(vector: X_i, vector_: X_j), power: 2))
        let k: Double = exp(self.theta[0]) * exp(-r / exp(self.theta[1]))
        return k
    }
    
    func Kernel_matrix() -> [[Double]] {
        let N: Int = self.X.count
        var K = [[Double]](repeating: [Double](repeating: 0, count: N), count: N)
        for i in 0..<N {
            for j in 0..<N {
                K[i][j] = self.kernel(X_i: self.X[i], X_j: self.X[j])
            }
        }
        K = calc.mpm(matrix: K, matrix_: calc.sxm(scalar: exp(self.theta[2]), matrix: calc.eye(n: N)))
        return K
    }
    
    func partial_kernel(X_i: [Double], X_j: [Double]) -> [Double] {
        let r: Double = calc.vsum(vector: calc.vpow(vector: calc.vmv(vector: X_i, vector_: X_j), power: 2))
        var partial_k = [Double](repeating: 0, count: self.theta.count)
        partial_k[0] = exp(theta[0]) * exp(-r / exp(self.theta[1]))
        partial_k[1] = exp(theta[0]) * exp(-r / exp(self.theta[1])) * exp(self.theta[1]) * r
        partial_k[2] = exp(theta[2])
        return partial_k
    }
    
    func partial_Kernel_matrix() -> [[[Double]]] {
        let N: Int = self.X.count
        var partial_K = [[[Double]]](repeating: [[Double]](repeating: [Double](repeating: 0, count: N), count: N), count: N)
        for i in 0..<N {
            for j in 0..<N {
                let partial_k = self.partial_kernel(X_i: self.X[i], X_j: self.X[j])
                for k in 0..<self.theta.count {
                    partial_K[k][i][j] = partial_k[k]
                }
            }
        }
        return partial_K
    }

    func log_likelihood(K: [[Double]], K_inv: [[Double]], det_K: Double) -> Double {
        let N: Double = Double(K.count)
        let L: Double = -(N/2)*log(2*Double.pi) - (1/2)*log(det_K) - (1/2)*calc.mdot(matrix: calc.mdot(matrix: calc.transpose(matrix: [self.y]), _matrix: K_inv), _matrix: [self.y])[0][0]
        return -L //負の対数尤度
    }
    
    func partial_L(K_inv: [[Double]]) -> [Double] {
        let dK: [[[Double]]] = self.partial_Kernel_matrix()
        var partial_L = [Double](repeating: 0, count: self.theta.count)
        let K_inv_dot_y: [Double] = calc.mdot(matrix: K_inv, _matrix: [self.y])[0]
        for i in 0..<self.theta.count {
            partial_L[i] = calc.trace(matrix: calc.mdot(matrix: K_inv , _matrix: dK[i])) - calc.mdot(matrix: calc.mdot(matrix: calc.transpose(matrix: [K_inv_dot_y]), _matrix: dK[i]), _matrix: [K_inv_dot_y])[0][0]
        }
        return partial_L
    }
}